






ARCH.625 A Re vel ati on : 4 +5 +6 +7 +8 +9 +10 +11 +12 +13 +14 +15 +16 +17 +18 +19 +20 +21 +22 +23 +24 +25 +26 +27 +28 +29 +30 +31 +32 +33 +34 +35 = 625 5 : 8 = 0 .625 [ golden section ]


ARCH.625 A Re vel ati on : 4 +5 +6 +7 +8 +9 +10 +11 +12 +13 +14 +15 +16 +17 +18 +19 +20 +21 +22 +23 +24 +25 +26 +27 +28 +29 +30 +31 +32 +33 +34 +35 = 625 5 : 8 = 0 .625 [ golden section ]


ARCH.625 A Re vel ati on : 4 +5 +6 +7 +8 +9 +10 +11 +12 +13 +14 +15 +16 +17 +18 +19 +20 +21 +22 +23 +24 +25 +26 +27 +28 +29 +30 +31 +32 +33 +34 +35 = 625 5 : 8 = 0 .625 [ golden section ]
ARCH.625 A Re vel ati on : 4 +5 +6 +7 +8 +9 +10 +11 +12 +13 +14 +15 +16 +17 +18 +19 +20 +21 +22 +23 +24 +25 +26 +27 +28 +29 +30 +31 +32 +33 +34 +35 = 625 5 : 8 = 0 .625 [ golden section ]








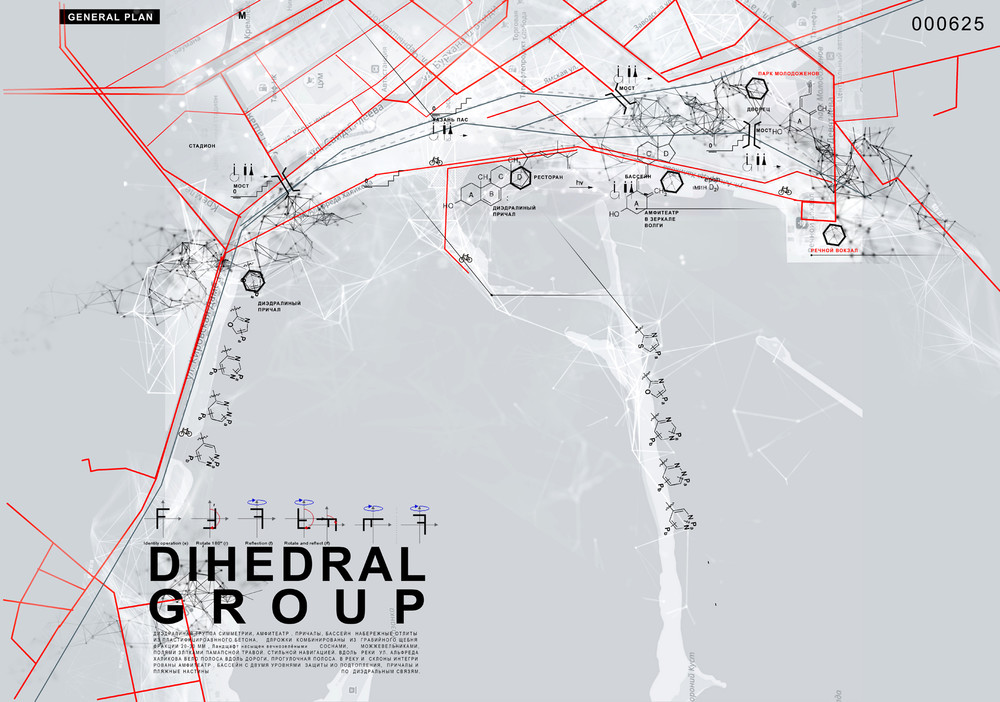
парк Молодожёнов Казань, Республика Татарстан, Россия 55.773986, 49.100467
ARCH.625 A Re vel ati on : 4 +5 +6 +7 +8 +9 +10 +11 +12 +13 +14 +15 +16 +17 +18 +19 +20 +21 +22 +23 +24 +25 +26 +27 +28 +29 +30 +31 +32 +33 +34 +35 = 625 5 : 8 = 0 .625 [ golden section ] / мода проходит, стиль остаётся ICON of STYLE
Инструменты:
ArchiCad/ Artlantis/ Photoshop /ДИЭДРАЛИНАЯ ГРУППА СИММЕТРИИ, АМФИТЕАТР , ПРИЧАЛЫ, БАССЕЙН НАБЕРЕЖНЫЕ ОТЛИТЫИЗ ПЛАСТИФИЦИРОАВННОГО БЕТОНА, ДOРОЖКИ КОМБИНИРОВАНЫ ИЗ ГРАВИЙНОГО ЩЕБНЯ ФРАКЦИИ 20-30 ММ , Ландщафт насыщен вечнозелёными СОСНАМИ, МОЖЖЕВЕЛЬНИКАМИ,ПОЛЯМИ ЗЛПКАМИ ПАМАПСНОЙ ТРАВОЙ. СТИЛЬНОЙ НАВИГАЦИЕЙ. ВДОЛЬ РЕКИ УЛ. АЛЬФРЕДАХАЛИКОВА ВЕЛО ПОЛОСА ВДОЛЬ ДОРОГИ, ПРОГУЛОЧНАЯ ПОЛОСА. В РЕКУ И СКЛОНЫ ИНТЕГРИРОВАНЫ АМФИТЕАТР , БАССЕЙН С ДВУМЯ УРОВНЯМИ ЗАЩИТЫ ИО ПОДТОПЛЕНИЯ, ПРИЧАЛЫ ИПЛЯЖНЫЕ НАСТИНЫ ПО ДИЭДРАЛЬНЫМ СВЯЗЯМ.
Диэдральная группа (группа диэдра) — группа симметрии правильного многоугольника, включающая как вращения, так и осевые симметрии[1]. Диэдральные группы являются простейшими примерами конечных групп и играют важную роль в теории групп, геометрии и химии. Хорошо известно и совершенно тривиально проверяется, что группа, образованная двумя инволюциями с конечным числом элементов в области определения является диэдральной группой. Правильный n-угольник имеет 2n различных симметрий: n поворотов и n осевых отражений, образующих диэдральную группу Dn. Если n нечетно, каждая ось симметрии проходит через середину одной из сторон и противоположную вершину. Если n четно, имеется n/2 осей симметрии, соединяющих середины противоположных сторон и n/2 осей, соединяющих противоположные вершины. В любом случае, имеется n осей симметрии и 2n элементов в группе симметрий. Отражение относительно одной оси, а затем относительно другой, приводит к вращению на удвоенный угол между осями. Изображения ниже показывают результат действия элемента D8 на дорожный знак Стоп: Как и для любого другого геометрического объекта, композиция двух симметрий правильного многоугольника снова будет симметрией. Таким образом, симметрии правильного многоугольника образуют конечную группу.Labeled Triangle Reflections.svg
Композиция двух отражений дает вращение.
Таблица Кэли показывает эффект композиции в группе D3 (симметрии правильного треугольника). R0 обозначает тождественное преобразование, R1 и R2 означает вращение против часовой стрелки на 120 и 240 градусов, S0, S1, и S2 означают отражение относительно осей, показанных на рисунке справа.
Диэдральная группа D2 порождается вращением r на 180 градусов, и симметрией s относительно оси X. Элементы D2 можно представить как {e, r, s, rs}, где e — тождественное преобразование и rs — симметрия относительно оси 'Y.Четыре элемента D2 (здесь ось X вертикальна)D2 изоморфна четверной группе Клейна.Для n>2 операции вращения и отражения относительно прямой не коммутативны и Dn не является абелевой. Например, в D4, вращение 90 градусов, а затем отражение дает совсем другой результат, нежели отражение, а затем вращение.
D4 не абелево (ось X здесь вертикальна).Таким образом, наряду с очевидным приложением к проблемам симметрии на плоскости, эти группы служат простейшими примерами неабелевых групп, и часто используются как контрпримеры для теорем, ограниченных абелевыми группами.
2n элементов Dn можно записать как e, r, r2, …, rn−1, s, r s, r2 s, …, rn−1 s. Первые n перечисленных элементов являются вращениями, остальные n — отражения относительно осей (все они имеют порядок 2). Результатом двух вращений или двух отражений будет вращение Результат вращения и отражения будет отражением.Таким образом, мы установили, что Dn является подгруппой O(2).
Однако, обозначение Dn используется для подгрупп SO(3), которые тоже являются группами типа Dihn: группа симметрии многоугольника, вложенного в трехмерное пространство (если n ≥ 3). Такие фигуры можно понимать как вырожденные тела (отсюда и название диэдрон